정의
- 자기 자신을 참조하는 재귀적 CTE(Common Table Expression)
- 전체 결과 집합을 얻을 때까지 데이터의 하위 집합을 반환하는 CTE
- MySQL 8.0 부터 추가된 신기능
용도
- 일정한 규칙을 가지는 연속적 숫자 또는 문자열의 시리즈 반환
- ex. 1, 2, 3, … / 피보나치 수열, 팩토리얼, (start_date ~ end_date)까지의 일련의 날짜 데이터 등
- 계층적 데이터를 반환하기 위한 목적
- ex. 조직도, 부모 - 자식 관계, 다단계 카테고리
구조

재귀 CTE는 크게 두 부분으로 나뉨
- 앵커 멤버(Anchor Member) : 재귀의 시작점으로, 보통 기본 조건을 정의. 이는 일반적인 CTE의 SELECT 문과 같으며, 여기서 반환된 결과가 재귀 호출의 기저 조건을 형성.
- 재귀 멤버(Recursive Member) : 앵커 멤버의 결과를 바탕으로 반복적으로 실행되는 부분. 이 멤버는 앵커 멤버의 결과를 참조하며, 재귀적으로 자기 자신을 호출하여 결과 집합을 확장.
- 두 부분은
UNION ALL연산자를 사용해 연결.UNION을 사용할 경우 중복 결과를 제거하지만, 재귀 CTE에서는 일반적으로UNION ALL이 사용되어 모든 결과를 포함하게 됨.
예시
-- 정수 시리즈(series) 만들기
WITH RECURSIVE natural_sequence AS (
SELECT 1 AS number
UNION ALL
SELECT number + 1 AS number
FROM natural_sequence
WHERE number < 4)
SELECT *
FROM natural_sequence;
- 첫 번째 반복: 앵커 멤버가 실행되며 number에 1을 포함시킴. 초기 데이터 세트로 사용된다.
SELECT 1 AS number
- 두 번째 반복:
- 이전 결과 (
number = 1)를 가져와WHERE number < 4조건을 평가. - 조건이 참이므로,
number + 1을 수행해 결과로 2를 생성.
- 이전 결과 (
- 세 번째 반복:
- 이전 결과 (
number = 2)를 가져와WHERE number < 4조건을 평가. - 조건이 참이므로,
number + 1을 수행해 결과로 3을 생성.
- 이전 결과 (
- 네 번째 반복:
- 이전 결과 (
number = 3)를 가져와WHERE number < 4조건을 평가. - 조건이 참이므로,
number + 1을 수행해 결과로 4를 생성.
- 이전 결과 (
- 다섯 번째 반복:
- 이전 결과 (
number = 4)를 가져와WHERE number < 4조건을 평가. - 이번에는 조건이 거짓이므로, 결과에 아무 것도 추가되지 않고 재귀 호출이 종료.
- 이전 결과 (
제한 사항 및 주의점
- 재귀적 SELECT 문에는 다음 구문이 포함되어서는 안됨
- SUM()과 같은 집계함수
- GROUP BY
- ORDER BY
- DISTINCT
- Window Function
- 제어되지 않은 재귀 호출로 인해 무한 루프에 빠질 위험이 있음
- 재귀 호출의 종료 조건을 명확하게 설정하는 것이 중요
문제 풀이
1. 정수 시리즈 만들기 : 1 ~ 10
WITH RECURSIVE natural_sequence AS (
SELECT 1 AS number
UNION ALL
SELECT number + 1 AS number
FROM natural_sequence
WHERE number < 10)
SELECT *
FROM natural_sequence;
- 쿼리의 실행순서 때문에, WHERE 조건이
WHERE number < 11이 아닌WHERE number < 10인 것에 주의
2. 팩토리얼(factorial) 계산하기
WITH RECURSIVE factorial(n, fact) AS (
SELECT 0, 1
UNION ALL
SELECT n+1, fact * (n+1)
FROM factorial
WHERE n < 10)
SELECT *
FROM factorial;
3. 피보나치 수열 계산하기
피보나치 수열: 첫째 및 둘째 항이 1이며 그 뒤의 모든 항은 바로 앞 두 항의 합인 수열이다. 처음 여섯 항은 각각 1, 1, 2, 3, 5, 8이다.
WITH RECURSIVE fibonacci (n, fib_n, next_fib_n) AS (
SELECT 1, 0, 1
UNION ALL
SELECT n + 1, next_fib_n, fib_n + next_fib_n
FROM fibonacci
WHERE n < 10)
SELECT *
FROM fibonacci;
4. 누락된 날짜를 추가한 보고서 작성
- 어떤 상점의 매출을 포함하는 간단한 테이블이 있다고 가정
- 해당 테이블로부터 날짜별 매출을 집계하는 판매 보고서를 뽑아내려고 한다

[ 예시 데이터 생성 ]
CREATE TABLE sales (
id INT AUTO_INCREMENT PRIMARY KEY,
order_date DATE,
product VARCHAR(20),
price DECIMAL(10, 2)
);
-- populate the table
INSERT INTO sales(order_date, product, price)
VALUES('2020-02-01','DVD PLAYER',100.50),('2020-02-01','TV',399.99),('2020-02-02','LAPTOP',1249.00),
('2020-02-04','DISHWASHER',500.00),('2020-02-04','TV',699.00),('2020-02-06','LAPTOP',990.50),('2020-02-06','HAIRDRYER',29.90),
('2020-02-06','GAME CONSOLE',299.00),('2020-02-07','BOOK',9.00),('2020-02-07','REFRIGERATOR',600.00);
-- let's run a query to generate the sales report by day
SELECT order_date, SUM(price) AS sales
FROM sales
GROUP BY order_date
ORDER BY 1;
- 그러나 판매 보고서에 누락된 날짜(해당 예제에서는 2월 3일, 2월 5일)가 존재하고, 판매가 없는 날짜도 매출=0 으로 포함해서 보고서를 생성하고 싶음! →
RECURSIVE CTE사용
[ 정답 쿼리 ]
WITH RECURSIVE dates(date) AS (
SELECT '2020-02-01' -- 보고서 상 start_date
UNION ALL
SELECT date + INTERVAL 1 DAY
FROM dates
WHERE date < '2020-02-07' ) -- 보고서 상 end_date
SELECT
dates.date
, COALESCE(SUM(price), 0) sales
FROM dates
LEFT JOIN sales ON dates.date = sales.order_date
GROUP BY dates.date
ORDER BY 1;
5. 계층적 데이터 순회
재귀 CTE를 이용해 계층적 데이터를 순회하는 예시를 크게 3가지 경우로 살펴본다.
1) 간단한 트리 : 조직도
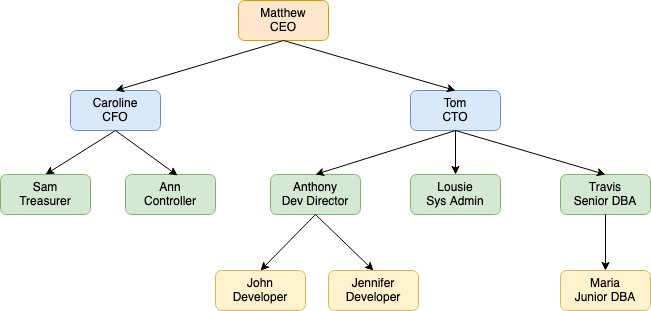
[ 예시 데이터 생성 ]
-- create the table
CREATE TABLE orgchart (
id INT PRIMARY KEY,
name VARCHAR(20),
role VARCHAR(20),
manager_id INT,
FOREIGN KEY (manager_id)
REFERENCES orgchart (id)
);
-- insert the rows
INSERT INTO orgchart VALUES(1,'Matthew','CEO',NULL),
(2,'Caroline','CFO',1),(3,'Tom','CTO',1),
(4,'Sam','Treasurer',2),(5,'Ann','Controller',2),
(6,'Anthony','Dev Director',3),(7,'Lousie','Sys Admin',3),
(8,'Travis','Senior DBA',3),(9,'John','Developer',6),
(10,'Jennifer','Developer',6),(11,'Maria','Junior DBA',8);
-- let's see the table, The CEO has no manager, so the manager_id is set to NULL
SELECT * FROM orgchart;
1. RECURSIVE CTE를 사용해 조직도에 따른 보고 체계(reporting chain)를 나타내보려고 한다

[ 정답 쿼리 ]
-- find the reporting chain for all the employees
WITH RECURSIVE reporting_chain(id, name, path) AS (
SELECT id, name, CAST(name AS CHAR(100))
FROM orgchart
WHERE manager_id IS NULL
UNION ALL
SELECT oc.id, oc.name, CONCAT(rc.path,' -> ',oc.name)
FROM reporting_chain rc
JOIN orgchart oc ON rc.id = oc.manager_id)
SELECT * FROM reporting_chain;
[ 풀이 ]
- 위의 코드에서 앵커멤버로 CEO인 Matthew를 설정하고, 재귀 멤버에서 상관의 id와 직원의 id와의 관계성을 이용하여 테이블 조인 조건으로 활용(
ON rc.id = oc.manager_id) - 주의할 점은 새로 지정한 path 필드에 대해서, CAST()함수를 통해 기존의 name 필드보다 더 많은 문자열을 저장할 수 있도록 명시적으로 데이터의 유형을 지정해줘야 한다는 것
-- 참고) path 필드에 대해 CAST()함수를 사용하지 않는 경우 에러 발생
WITH RECURSIVE reporting_chain(id, name, path) AS (
SELECT id, name, name
FROM orgchart
WHERE manager_id IS NULL
UNION ALL
SELECT oc.id, oc.name, CONCAT(rc.path,' -> ',oc.name)
FROM reporting_chain rc
JOIN orgchart oc ON rc.id=oc.manager_id)
SELECT * FROM reporting_chain;
-- ERROR 1406 : Data too long for column 'path' at row 12. 위에서 나타낸 보고 체계(reporting chain)에 더해 직원의 level까지 나타내는 쿼리

- 직원의 level은 거쳐야 하는 보고체계의 단계와 일치하며, 아래의 쿼리를 통해 재귀 멤버의 반복 횟수와도 연관성이 있음을 알 수 있다
[ 정답 쿼리 ]
-- find the (reporting chain + level) for all the employees
WITH RECURSIVE reporting_chain(id, name, path, level) AS (
SELECT id, name, CAST(name AS CHAR(100)), 1
FROM orgchart
WHERE manager_id IS NULL
UNION ALL
SELECT oc.id, oc.name, CONCAT(rc.path,' -> ',oc.name), rc.level+1
FROM reporting_chain rc
JOIN orgchart oc ON rc.id=oc.manager_id)
SELECT * FROM reporting_chain
ORDER BY level;
2) 복잡한 트리 : 가계도
조부모, 부모, 아들이 있는 다음의 가계도를 가정해보자

[ 예시 데이터 생성 ]
CREATE TABLE genealogy (
id INT PRIMARY KEY,
name VARCHAR(20),
father_id INT,
mother_id INT,
FOREIGN KEY (father_id)
REFERENCES genealogy (id),
FOREIGN KEY (mother_id)
REFERENCES genealogy (id)
);
-- populate the table
INSERT INTO genealogy VALUES(1,'Maria',NULL,NULL),
(2,'Tom',NULL,NULL),(3,'Robert',NULL,NULL),
(4,'Claire',NULL,NULL),(5,'John',2,1),
(6,'Jennifer',2,1),(7,'Sam',3,4),
(8,'James',7,6);
SELECT * FROM genealogy;
1. id = 8인 James의 조상과 그에 따른 관계를 RECURSIVE CTE로 찾아내보려고 한다

[ 정답 쿼리 ]
-- Let’s find all of James’s ancestors and the relationship:
WITH RECURSIVE ancestors AS (
SELECT *
, CAST('son' AS CHAR(20)) AS relationship
, 0 level
FROM genealogy
WHERE name='James'
UNION ALL
SELECT
g.*
, CASE WHEN g.id = a.father_id AND level=0 THEN 'father'
WHEN g.id = a.mother_id AND level=0 THEN 'mother'
WHEN g.id = a.father_id AND level=1 THEN 'grandfather'
WHEN g.id = a.mother_id AND level=1 THEN 'grandmother'
END
, level + 1
FROM genealogy g, ancestors a -- implicit join
WHERE g.id = a.father_id OR g.id = a.mother_id) -- same with ON in JOIN query
SELECT *
FROM ancestors;
[ 풀이 ]
- 위의 코드에서 앵커 멤버로 아들(son)인 James를 설정하고 James의 level을 0으로 설정
- 재귀 멤버에서 부모의 id와 본인의 id와의 관계성을 이용하여 테이블 조인 조건으로 활용(
g.id = a.father_id OR g.id = a.mother_id)- 참고로 해당 쿼리는 암시적 조인으로 구성된 쿼리문이며, 암시적 조인은 명시적 조인으로 치환가능
-- 암시적 조인
FROM genealogy g, ancestors a
WHERE g.id = a.father_id OR g.id = a.mother_id
-- 명시적 조인
FROM genealogy g
JOIN ancestors a ON g.id = a.father_id OR g.id = a.mother_idrelationship필드는 CASE WHEN문을 활용- 조건 1) 아빠쪽인지, 엄마쪽인지를 구분하기 위해
father_id,mother_id활용 - 조건 2) 앵커 멤버(여기서는 James)의 부모인지 조부모인지를 알기위해
level활용
- 조건 1) 아빠쪽인지, 엄마쪽인지를 구분하기 위해
level필드는 재귀 멤버의 반복 횟수에 따라 값이 정해짐
2. 동일한 쿼리를 사용하지만 초기 조건을 변경함으로써, 다른 사람의 조상과 관계에 대해 나타낼 수 있음을 보여줌(해당 예제는 Jennifer의 조상 찾기)
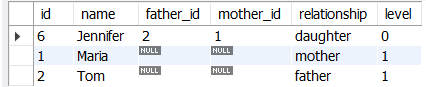
[ 정답 쿼리 ]
-- 동일쿼리, but 초기 조건 변경(해당 예제는 Jennifer의 조상 찾기)
WITH RECURSIVE ancestors AS (
SELECT *
, CAST('daughter' AS CHAR(20)) AS relationship
, 0 level
FROM genealogy
WHERE name='Jennifer'
UNION ALL
SELECT
g.*
, CASE WHEN g.id=a.father_id AND level=0 THEN 'father'
WHEN g.id=a.mother_id AND level=0 THEN 'mother'
WHEN g.id=a.father_id AND level=1 THEN 'grandfather'
WHEN g.id=a.mother_id AND level=1 THEN 'grandmother'
END
, level + 1
FROM genealogy g, ancestors a
WHERE g.id=a.father_id OR g.id=a.mother_id)
SELECT *
FROM ancestors;
3) 그래프 : 기차 노선도
- 아래는 이탈리아의 기차 경로를 나타내는 구조도이다
- 단방향 및 양방향 연결에 유의.
origin은 출발지,destination은 목적지,distance의 단위는 km - 아래의 train_route 테이블을 기반으로 다음의 문제들을 풀어볼 예정
- 밀라노(MILAN)을 출발지로 갈 수 있는 모든 기차 목적지 반환
- 밀라노(MILAN)에서 시작하여 가능한 모든 경로와 각 경로의 총 길이
- 최단 경로 찾기(from MILAN to NAPLES)

[ 예시 데이터 생성 ]
CREATE TABLE train_route (
id INT PRIMARY KEY,
origin VARCHAR(20),
destination VARCHAR(20),
distance INT
);
-- populate the table
INSERT INTO train_route VALUES(1,'MILAN','TURIN',150),
(2,'TURIN','MILAN',150),(3,'MILAN','VENICE',250),
(4,'VENICE','MILAN',250),(5,'MILAN','GENOA',200),
(6,'MILAN','ROME',600),(7,'ROME','MILAN',600),
(8,'MILAN','FLORENCE',380),(9,'TURIN','GENOA',160),
(10,'GENOA','TURIN',160),(11,'FLORENCE','VENICE',550),
(12,'FLORENCE','ROME',220),(13,'ROME','FLORENCE',220),
(14,'GENOA','ROME',500),(15,'ROME','NAPLES',210),
(16,'NAPLES','VENICE',800);
SELECT * FROM train_route;
1. MILAN을 출발지로 갈수 있는 모든 기차 목적지 반환

[ 정답 쿼리 ]
WITH RECURSIVE train_destination AS (
SELECT origin AS dest
FROM train_route
WHERE origin='MILAN'
UNION -- UNION ALL이 아닌 UNION을 써야 함
SELECT tr.destination
FROM train_route tr
JOIN train_destination td ON td.dest = tr.origin)
SELECT *
FROM train_destination;
[ 풀이 ]
- 위의 코드에서 앵커 멤버로 출발지인 MILAN를 지정
- 재귀 멤버에서 이전 재귀(또는 앵커 멤버)의 목적지(dest)와 현재 재귀의 출발지(origin)의 관계성을 이용하여 테이블 조인 조건으로 활용(
ON td.dest = tr.origin) - 주의할 점은
UNION ALL이 아닌UNION을 써야 함- 지금까지의 문제들에서는 모두 UNION ALL을 써왔지만 해당 문제는 UNION ALL을 쓰게 되면 무한 루프에 빠지게 됨
- MILAN -> FLORENCE -> VENICE와 같은 circle 때문에 중복값이 무한으로 생성되기 때문

2. 밀라노에서 시작하여 가능한 모든 경로와 각 경로의 총 길이
- 밀라노에서 시작해서 가능한 모든 경로 & 그 길이를 구하려고 한다
- 단, 한번 갔던 목적지는 다시 지나치지 않는다는 조건 필요(무수히 많이 늘어나는 경로를 막기위해)

WITH RECURSIVE paths (cur_path, cur_dest, tot_distance) AS (
SELECT
CAST(origin AS CHAR(100))
, CAST(origin AS CHAR(100))
, 0
FROM train_route
WHERE origin = 'MILAN'
UNION
SELECT
CONCAT(P.cur_path, ' -> ', T.destination)
, T.destination
, P.tot_distance + T.distance
FROM paths P
JOIN train_route T
ON P.cur_dest = T.origin
AND NOT FIND_IN_SET(T.destination, REPLACE(P.cur_path,' -> ',','))
-- 현재 경로(P.cur_path)에서 이미 방문한 도시를 다시 방문하지 않도록 하기 위한 조건
)
SELECT *
FROM paths;
[ 풀이 ]
- 이 쿼리문에서 가장 중요한 부분은 재귀 멤버에서의 JOIN 조건
ON P.cur_dest = T.origin- 이 부분은 현재 경로의 마지막 목적지(
P.cur_dest)가 다음 가능한 경로의 출발지(T.origin)와 일치하는 경우를 찾게 됨. 즉, 현재 경로에서 이어질 수 있는 다음 경로를 찾는 것.
- 이 부분은 현재 경로의 마지막 목적지(
AND NOT FIND_IN_SET(T.destination, REPLACE(P.cur_path,' -> ', ',' )- 현재 경로(
P.cur_path)에서 이미 방문한 도시를 다시 방문하지 않도록 하기 위한 조건.REPLACE(P.cur_path,' -> ', ',')- 이 함수는 현재 경로에서 도시 이름들 사이의 구분자인 ' -> '를 쉼표(,)로 바꿈.
- 이렇게 하면 FIND_IN_SET 함수에서 사용하기 쉬운 형식의 문자열이 됨.
FIND_IN_SET(T.destination, REPLACE(P.cur_path,' -> ',','))- 이 함수는 바뀐 문자열에서 현재 경로의 도시 목록(
P.cur_path)에 다음 목적지(T.destination)가 포함되어 있는지 확인. - 포함되어 있으면 해당 도시의 위치를 반환하고, 포함되어 있지 않으면 0을 반환.
- 이 함수는 바뀐 문자열에서 현재 경로의 도시 목록(
NOT FIND_IN_SET(T.destination, REPLACE(P.cur_path,' -> ',','))- 이 조건은 FIND_IN_SET 함수의 결과가 0인 경우를 찾게 됨. 즉, 현재 경로에 다음 목적지(
T.destination)가 포함되어 있지 않은 경우를 의미.
- 이 조건은 FIND_IN_SET 함수의 결과가 0인 경우를 찾게 됨. 즉, 현재 경로에 다음 목적지(
- 현재 경로(
3. 최단 경로 찾기(from MILAN to NAPLES)
[ 풀이 ]
- 2번의 가능한 모든 경로찾기 쿼리문을 기반으로 최단 경로도 찾아낼 수 있음
- 아래의 쿼리문은
- 밀라노(MILAN)에서 출발하는 모든 가능한 경로를 구한 뒤
- 출력 조건(WHERE 절)에서 최종 도착지가 나폴리(NAPLES)인 경우를 필터링하고
- 전체 이동거리(
tot_distance)에 대해 오름차순으로 정렬한 뒤LIMIT 1로 최단 거리만 출력


[ 정답 쿼리 ]
WITH RECURSIVE paths (cur_path, cur_dest, tot_distance) AS (
SELECT
CAST(origin AS CHAR(100))
, CAST(origin AS CHAR(100))
, 0
FROM train_route
WHERE origin='MILAN'
UNION
SELECT
CONCAT(P.cur_path, ' -> ', T.destination)
, T.destination
, P.tot_distance + T.distance
FROM paths P
JOIN train_route T
ON P.cur_dest = T.origin AND
NOT FIND_IN_SET(T.destination, REPLACE(P.cur_path,' -> ',','))
)
SELECT *
FROM paths
WHERE cur_dest='NAPLES'
ORDER BY tot_distance ASC LIMIT 1;
관련된 프로그래머스 문제
GROUP BY - 입양 시각 구하기(2) - LEVEL 4
SELECT - 특정 세대의 대장균 찾기 - LEVEL 4
References
Introduction to MySQL 8.0 Recursive Common Table Expression (Part 2)
Intro to MySQL 8 Recursive Common Table Expression. SQL is generally poor at recursive structures, but it's now possible on MySQL writing recursive queries.
www.percona.com
'SQL' 카테고리의 다른 글
| [프로그래머스] 9주차 MySQL 스터디 2 (1) | 2024.06.05 |
|---|---|
| [프로그래머스] 9주차 MySQL 스터디 1 (0) | 2024.06.05 |
| [프로그래머스] 8주차 MySQL 스터디 2 (0) | 2024.06.04 |
| [프로그래머스] 8주차 MySQL 스터디 1 (2) | 2024.06.04 |
| [프로그래머스] 7주차 MySQL 스터디 2 (1) | 2024.06.04 |
